Atomic force microscopy (AFM) is an ideal technique to characterise topography, as well as many other properties, of polymer films and artifacts. AFM has several advantages over electron microscopy in this regards. For instance, most polymers are insulators, and would therefore need to be coated for SEM observation, potentially changing their texture. AFM also does not need a thin sample, as TEM does.
There are many different experiments and modes appropriate for polymer samples. For good reviews see the bibliography at the end of the this article, or the longer article in my book. This article discusses two common types of measurements of polymer samples by AFM.
Phase imaging
Modes such as phase imaging are very useful for polymer composites, and copolymers since they consist of mixed materials, and the distribution of the phases is usually critical for their properties.
As described in section 3.2.3.2 of the book, phase imaging is sensitive to viscoelastic properties of the sample and to tip-sample adhesion. This means that many materials can be differentiated by phase imaging Because of its ability to distinguish many materials, phase imaging has been applied to an enormous number of samples, just some examples include differentiation of semiconductor films, nanoparticle characterisation and counting, observation of spherulites in polymer crystallisation, polymer blend and composite composition, protein adsorption to biomaterials, self assembled monolayers, and many more systems.
Phase imaging is particularly useful for distinguishing features in polymer films which do not exhibit great height contrast. For example, in the image below.

Hardness measurements of polymers
Polymers have been a particular focus of AFM nanoindentation studies. One reason for this is that many composite polymeric materials exhibit nanoscale domains. Examples include polymers with fillers or other added particulate materials, and block copolymers. Measurement of the stiffness of such domains can help to understand their contributions to the overall mechanical properties of the bulk materials. In some cases, materials are added to a polymer specifically to change the mechanical properties, such as adding stiffness, or increasing elasticity. The nature of the interface between the reinforcing material and the continuous polymer matrix can be very important for the mechanical properties of the materials. AFM-based nanoindentation is ideal to probe the mechanical studies of nanoscale phases, as well as their interfaces. An example of this is illustrated in the figure below.
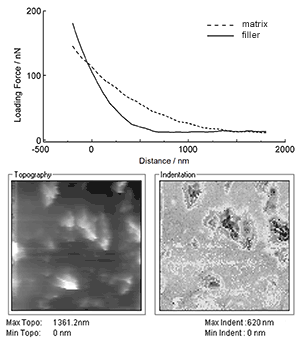
Results of nanoindentation on polymer composite. Raw forces curves (top), height image (below left), Indentation map (below right). See Eaton and West.
In this case, the material under study was a commercial silicone paint, which included include large calcium carbonate filler particles. AFM-based nanoindentation measurements were made of the polymer surface via a force-curve mapping routine. When measuring curves over the raised features seen on the surface, they were shown to be considerably stiffer than the surrounding polymer matrix, as is seen in the image of indentation distance. Interestingly, a softer region seems to surround each hard particle, possibly indicating some problems at the matrix-filler interface. This highlights a strength of AFM-based nanoindentation for analysis of polymer posited; namely the direct measurement of mechanical property variation at the nanoscale.
Conclusions:
A few other common applications of AFM in polymer science include studies of cyrstallisation, heat-dependent properties, and frictional properties. AFM makes an extremely useful and versatile tool in polymer science.
Bibliography
-
Atomic Force Microscopy, Eaton and West, Oxford, 2010, Chapter 7.
-
Scanning Probe microscopy in Industrial Applications, ed. D. Yablon, Wiley, 2014, Chapter 9.
-
Vanlandingham, M. R. et al., Nanoscale indentation of polymer systems using the atomic force microscope. Journal of Adhesion 1997, 64, (1-4), 31-59
-
Eaton, P., et al., Combined Nanoindention and Adhesion Force Mapping Using the Atomic Force Microscope: Investigations of a Filled Polysiloxane Coating, Langmuir, 18(25) 10011-10015 (2002).
This article is an edited extract from "Atomic Force microscopy" by Peter Eaton and Paul West, 2010, OUP. For more details, click here.
All Images and Text copyright Peter Eaton 2010-2016.

